RSS

Why the Global Economy is About to Crash - Global Economic Crash, Economic Crisis, Stock Market Crash

Why the Global Economy is About to Crash

And What You Can Do About It

The global economy (meaning modern life as we know it) is about to totally, permanently, and unrecoverably crash. I estimate that the crash will happen in the next 1-15 years. (Though potentially it could happen in the next day of trading).

Even today, very few people realise just how close we really are to the end (in terms of our modern global economy and high-tech way of life)...

Many people are unaware, but in the fall of 2008 [that's the spring of 2008 in the southern hemisphere], we were within a few hours of the entire banking system shutting down. Banks were on rolling notice and were within hours of being locked and electronic commerce turned off.

David Morris, Urban Survival Guide, p123.

It pains me deeply to announce that, despite the massive government rescue, yesterday’s [2008] collapse of Citigroup could ultimately lead to a shutdown of the global banking system... On October 11, 2008, a single statement hit the international wire services: "Intensifying solvency concerns about a number of the largest U.S.-based and European financial institutions have pushed the global financial system to the brink of systemic meltdown." This statement was not the random rant of a gloom-and-doomer on the fringe of society. Nor was it excerpted from a twentieth century history book about the Great Depression. It was the serious, objective assessment announced at a Washington, D.C. press conference by the Managing Director of the International Monetary Fund (IMF).

We rarely saw a run on the bank by individuals. Rather, it was uninsured institutional investors — banks, pension funds and others — that jumped ship long before most people even realized the ship was sinking.

Dr. Martin D. Weiss, Global Research.

I will be writing a lot more about this (and what can be done about it) on survival.org.au in the next few months, so stay tuned if this is something that you are interested in. I will probably also be updating and fine tuning this page (to make it better).

Why Is The Crash 100% Guaranteed to Happen?

There are two reasons which combine to create the conditions that make the crash 100% inevitable.

The global economy (and all modern domestic economies) require ongoing economic growth to be able to exist.
Because of resource availability constraints, this ongoing economic growth can no longer exist in the long term.

Ongoing Economic Growth

I've already written a lot on another page about why we need ongoing economic growth in order for our modern way of life (and economy) to exist. The page is a bit long-winded, though its worth a skim if you are interested in the why's of it. For a better explanation of growth (and some of the issues that come out of our need for it), watch this excellent online video by Professor Emeritus Al Bartlett.

I think that probably, for most economists, saying something like "there can be no more growth (as in economic growth), ever" would be like saying to a Christian that Jesus Christ never really existed, or to a Buddhist that Buddha never really existed, or to a Muslim that Mohammed never really existed... (you get the idea). What I mean is, it's a pretty big deal.

These problems [of resource depletion, continued population growth, declining per-capita food production, global climate change and other signs of environmental degradation, unsustainable levels of US debt and a potential dollar collapse, and international political instability] are related to each other in complex, often mutually reinforcing ways. Taken together, they constitute the most severe challenge our species has ever faced. They represent not merely a likely culmination of human history; in their ongoing and potential environmental impacts, they also may collectively signal one of the most momentous events in all of geological time.

Richard Heinberg, Powerdown.

Resource Availability Constraints

The first of the resource availability constraints that I'm talking about is what people call peak oil. There is a lot written about this already on the internet, including on this site. To summarise what peak oil is in one paragraph, peak oil is the point in time at which the rate of extraction of crude oil reaches its all-time high. After the peak is passed, forever after (and this means forever) there will always be less and less oil available to the market.

There are still people in the media who refer to peak oil as a theory. The word "theory" here is used to imply something that has been suggested, but not proved for certain. Peak oil was a theory in 1956 when M. King Hubbert predicted that the United States domestic oil production would peak in about 1970, and then forever after go into decline. Peak oil stopped being a theory in 1970 when this came true just as he had predicted.

Since then, country after country has already peaked and gone into terminal decline. Australia peaked in 2000 and has been in decline ever since (and will be forever after). There is no-one disputing the historical statistics for the amounts of oil extraction, so it is quite easy to look back at the numbers and see that peak oil (for individual countries) is completely, 100% real and verifiable.

Global peak oil is where peak oil happens for the Earth as a whole. Since there is not an infinite number of countries in the world, and there is no single country with an infinite amount of oil, it follows logically that as one country after another peaks and goes into decline, at some point the whole world will peak, and then go into decline. There is absolutely no doubt whatsoever that peak oil (in the global sense) is real.

Finally, even if there was an infinite amount of oil, there are a great many other critical resources that are also peaking at around this time, and about to go into decline.

It's Not About Money

Economists (and the regular mass media news broadcasts) like to talk a lot about money, markets, and economics. In the end, it will appear to many to be those things that "cause" the crash. However money is just bits of paper and numbers in computers. It makes a lot of difference to individuals' lives — but on the global scale, it matters relatively little how much money there is, or even who has it, in terms of real things that are available.

Things such as food, water, housing might be brought to you personally by people who are motivated by the flow of money, and in this sense it does obviously affect you. However the total amount of real, physical resources available in the world is unaffected by money or by markets.

It could be said that individual people are (in a sense) made rich or poor by the flow of money. However, no matter how you redistribute money, the entire Earth as a whole will still be exactly the same in terms of the total amount of physical resources that exist. Since the problem we are now facing is about the total amount of physical resources that exist, no amount of manipulation of monetary systems will have any permanent effect on the problem.

I'll repeat this point, since there will be a lot of people who don't get this, both now and for many years after the real crisis gets underway. Once enough of the Earth's physical natural resources are used up, no amount of changes to the monetary system (or any other economic changes) will make any difference to the resource shortage in the long term and in the big picture.

The reason that some people have trouble understanding this point is because they are used to thinking of so much of their everyday lives in terms of the flow of money. People's life experience tells them that money can buy almost anything. Perhaps apart from invisible and intangible things like "love", money can pretty well buy anything. (With all due respect to Sir Paul McCartney, in many people's life experience, a lot of the time money can even buy intangibles, including love).

When people watch the mainstream media, it seems like almost all of the big issues in the world are one way or another about money, trade, commerce, or politics. The actual, physical, amounts of resources that are needed, and the amounts that are remaining, are almost never mentioned. For example, the price of oil is stated in nearly every news broadcast, but the amounts of oil that are used each day, and remaining, are almost never mentioned. Occasionally new discoveries of resources are mentioned, but this is usually because the discovery makes some companies' share price go up, and is being mentioned mainly (or entirely) because of its effect on the flow of money.

Because of this bias of exposure in the media, people are not used to thinking of real actual physical natural resources as important (or even thinking of them at all). When in fact they are the underlying basis for all trade, commerce, and politics.

Another effect of this fact is that the upcoming crash is not the banks fault, or the government's fault. It's nobody's fault and everybody's fault.

Oil is Peaking Right Now

The balance of available evidence is that oil is peaking right now. That is, give or take a few years, we are basically at the all time high in terms of rate of oil extraction.

The fact that we are at (approximately) the highest point so far in history is obvious from the statistics. The graph indicates that the global output of oil has been approximately constant since 2005. Note also that the scale on the left hand side of the graph does not start from zero at the bottom of the graph. This has the effect of exaggerating the ups and downs in the graph. If it were drawn to scale, it would look a lot flatter than it does below.

Whether or not this means that we are at the all-time high of oil extraction (or, conversely, whether this graph can still go up a lot in the future, as is required for the global economy to continue to exist for any length of time), is something that you can read about elsewhere (it takes more than a paragraph to explain). For here I will just say that I have been following this issue on and off since 1979, and in detailed research since about 2001, and I am convinced that it is unlikely there can be no more short-term significant increases in oil production, and almost completely impossible that there will be long term ones. I have more of an explanation of this here.

We are now in the period in history that is referred to as the "petroleum plateau", the flat-ish spot at the top of the all-time oil extraction curve. The flat spot could potentially continue for a while longer (I would estimate perhaps another decade, maximum, and probably less than that), or it could end this week.

This flat spot is characterised by a period in which global economic growth is at first slowed, then capped to a standstill (approximately zero growth). The initial effects of this in global (and domestic) financial markets are quite apparent from watching regular news broadcasts.

What it important to realise is that even if oil production (i.e. extraction) could continue forever at this current "petroleum plateau" rate (which it can't), that would still not be enough to stop the global economy from completely crashing. The amount of oil that we use globally needs to grow, and keep growing (in the long term scale, not just for a year or two), in order for our modern economies to continue to exist.

Peak Oil and World Population

World Crude Oil Production (Source: theoildrum.com)

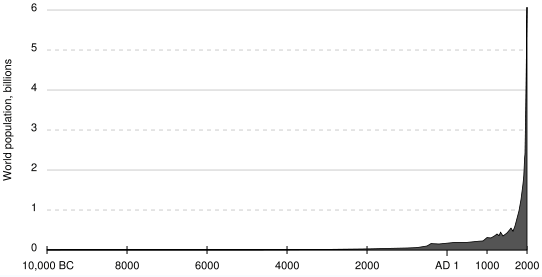
If you want to see future versions of this graph, Google "oil drum oilwatch monthly" (without the quotes) and click on the most recent month that comes up. Then scroll down to the graphs for World Crude Oil Production and World Liquid Fuels Production.

According to The Oil Drum, 'As everyone knows, there is never a post on The Oil Drum that the entire staff agrees on. Nonetheless, Tony bases his findings on solid research, and a staff survey shows that most agree with a 2008 peak. A post discussing whether an alternate scenario with a second later peak might be feasible is planned for later. World oil production peaked in 2008 at 81.73 million barrels/day (mbd) shown in the chart below. This oil definition includes crude oil, lease condensate, oil sands and natural gas plant liquids. If natural gas plant liquids are excluded, then the production peak remains in 2008 but at 73.79 mbd. However, if oil sands are also excluded then crude oil and lease condensate production peaked in 2005 at 72.75 mbd.'

According to Wikipedia, 'Worldwide oil production, including oil from oil sands, reached an all-time high of 73,720,000 barrels per day (11,721,000 m3/d) in 2005. By 2009, production had declined to 72,260,000 barrels per day (11,488,000 m3/d). In Feb 2010 the US military's Joint Forces Command issued the Joint Operating Environment 2010 warning US military commands "By 2012, surplus oil production capacity could entirely disappear, and as early as 2015, the shortfall in output could reach nearly 10 million barrels per day."'

The Real, Underlying Problem — It's Not Just Oil That's Running Out

It's not only oil that is peaking at around this time in history.

Have a look at the graph of world population below:

Peak Oil and World Population

World Population (Source: Wikipedia)

Considering the graph above, notice that the shaded area under the graph gives an approximate idea of the amount of resources that will be consumed by those people.

Consider also that modern people use far more resources per person than people did in the old days. (For example, the average person in the USA has 70 times the ecological footprint of the average person in Bangladesh). Therefore, the closer you get to the right of the graph, the more resources are needed per person. Which means the extreme increase in population on the right of the graph is even more extreme in terms of resources.

What this means is that in order for business as usual to continue for just another generation (say 30-40 years), the amount of resources the world will need for just those next few decades is roughly equal to (or greater than) the total amount of resources that have ever been consumed, ever, in the history of the human race.

If this seems hard to believe, the online video by Al Bartlett explains quite well how, in a situation of exponential growth, the area under the graph for just one doubling period exactly equals the area under the entire rest of the graph.

This is why it seems like "everything" is running out now, or about to run out. Because it is.

When you consider also that we have already used more than half of the available oil, over 75% of the topsoil that existed in the 1500s is now gone, and the human race now uses over 40% of the total resources available to all species on the planet, and our global economy must continue to grow in order for it to continue to exist, it is clear that we are about to run into some big changes.

In the 24 hours since this time yesterday, over 200,000 acres of rainforest have been destroyed in our world. Fully 13 million tons of toxic chemicals have been released into our environment. Over 45,000 people have died of starvation, 38,000 of them children. And more than 130 plant or animal species have been driven to extinction by the actions of humans. (The last time there was such a rapid loss of species was when the dinosaurs vanished.) And all this just since yesterday.

Thom Hartmann, The Last Hours of Ancient Sunlight.

What To Do About It

The sooner you start on this, the better (for you and, to some extent, for everyone else).

If you find that you can't deal with it (at first), whatever that means for you, you are going to be much better off going through this phase of reality sinking in before things start to really change. While there is still all the conveniences and benefits of modern life and of our availability of technology, information, tools, social stability, and so on.

It's not something that is outright impossible to deal with, since people have been living in ways other than our current modern high-tech lifestyle for the whole of human history up till very recent times.

See here for more: What To Do About the Upcoming Economic Crash

Summary

The practical outcome of this is that the modern way of life we have all become accustomed to is about to change on a major scale. This website (along with many others on the internet) is an attempt to help people to come to terms with these changes, and to take appropriate action in response.